How Far Would Student Loan Borrowers Go to Have Their Student Loan Debt Erased?

This post contributed by Mike Brown of LendEDU.

Student loan debt is at an all-time high in the United States; currently, the nationwide outstanding student loan debt is a whopping $1.61 trillion. 

How does this stack up against other classes of consumer debt? It’s the second largest form of outstanding debt in the U.S. behind only mortgage debt, but surpassing other collective debt like that from credit cards, auto loans, or medical expenses. 

In 2020, there are 44.5 million student loan borrowers in the U.S. The average student loan borrower owes a considerable $28,565 in student loan debt, while the average graduate owes $16,649 in student debt upon leaving their college campus with a diploma in hand. Speaking of which, 57% of graduates from the Class of 2018 walked away from school with some amount of student loan debt. 

For most student loan borrowers, this student loan debt will be getting repaid for more than a decade. The Federal Reserve estimates that the average monthly student loan payment amongst borrowers is $393, while the median monthly student loan payment is $222. 

Regardless, that’s a considerable sum of money to be forking over month after month for 10 years at a minimum, and many young Americans struggle with the financial commitment. Approximately 10.9% of all student loan debt is either 90 days delinquent or entirely in default, which means the loans have stopped getting repaid. 

The costly student loan debt obligation faced by so many young consumers has kept many from moving forward financially. With monthly student debt payments taking up quite a bit of income, it can be tough for these folks to hit milestones like buying a car, buying a house, getting married, or starting a family. 

With such a tremendous financial burden being placed on student loan borrowers these days, LendEDU wanted to examine how far this group would be willing to go to have their student loan debt completely forgiven. 

To do this, LendEDU employed the online surveying services of Pollfish to ask 1,000 adult Americans with some amount of student loan debt what they would do if it meant their student debt was erased in return. 

LendEDU’s report posed a series of 11 hypothetical scenarios to respondents in which they had to decide if they would go through with each imaginary scenario to wipe away their student loan debt. The answers, while sometimes humorous, may shock you.

The Six Things Borrowers Would Be Most Willing to Do For Student Loan Forgiveness

For reference, each question in the Pollfish survey was phrased like this: “Would you {insert scenario here} if it meant all of your student loan debt was forgiven?”

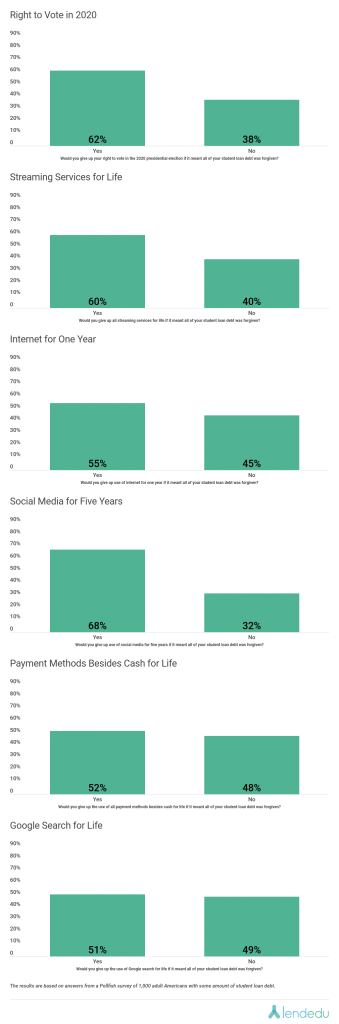
Student loan borrowers in the U.S. were most willing to part with social media for the next five years if it meant their student loan debt was forgiven. 68% of respondents were ready to go through with that hypothetical scenario, while 32% were not quite ready to rid themselves of Instagram, Twitter, Facebook, or whatever other platforms. 

Next, 62% of Pollfish respondents were ready to give up their vote in the upcoming 2020 presidential election, while 32% were not. The next hypothetical scenario followed closely in terms of the answer breakdowns; 60% of poll participants would give up all streaming services, like Netflix or Disney+, for life to erase their student loan debt, while 40% would not do that. 

55% of student loan borrowers were ready to part ways with internet access for one year, while 45% were not. When it came to giving up all payment methods besides cash for life for student loan forgiveness, 52% of respondents would do this and 48% would not.

Finally, 51% of participants in the LendEDU survey indicated they would give up Google Search for life for student loan forgiveness, while 49% answered the opposite.

The Five Things Borrowers Would Be Least Willing to Do For Student Loan Forgiveness

On the opposite end of the spectrum, the thing student loan borrowers were least willing to do in order to have their student loan debt completely forgiven was giving up hot showers for the next 25 years. Only 17% of respondents were ready to make this sacrifice, while 83% were not.

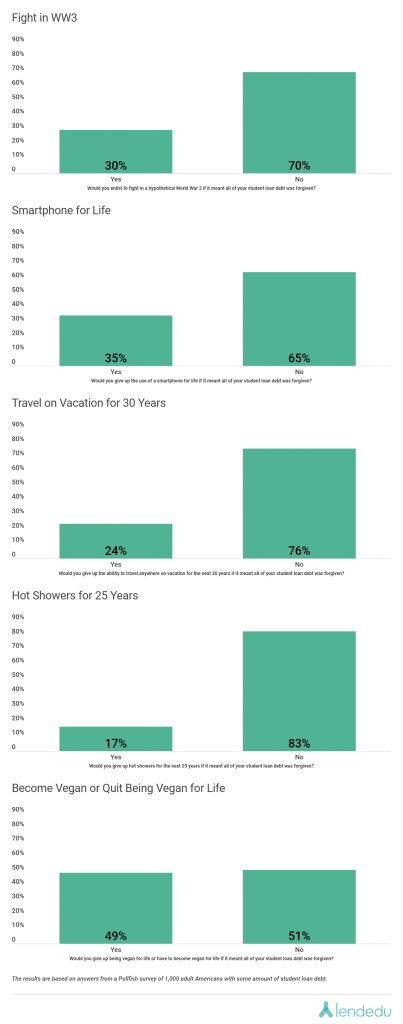
After that, only 24% of Pollfish respondents said they would give up the ability to travel anywhere on vacation for the next 30 years for student loan forgiveness, while 76% answered with the opposite. When it came to fighting in a hypothetical World War 3, only 30% of student loan borrowers would do this to erase their student loan debt, while 70% would not.

Further, just 35% of student loan borrowers would give up their smartphone for life for forgiveness compared to the 65% of respondents that were not willing to do this. And finally, 49% of borrowers would either become vegan or give up being vegan for life if it led to student loan forgiveness, while 51% could not agree to this.

Using Pollfish, LendEDU has gathered original data helpful to understanding consumers, developing insightful reports, and offering the right solutions to their customer base. Want great data of your own? Create an account and get started.